Тема: Проекційне креслення: способи зображення предметів.
Прямокутні проекції, їх назви, площини проекцій і утворення
Мета:
Навчальна: Дати учням
поняття про способи зображення предметів. Ознайомити з прямокутними проекціями, назвами, площинами проекцій
та способами їх утворення.
Розвиваюча: Сприяти
розвитку логічного мислення учнів через проведення таких операцій як аналіз,
порівняння, систематизація. Розкрити їх творчі здібності.
Виховна: Привити слухачам
любов до предмету. Стимулювати учнів до виховання старанності, наполегливості,
бажання творчо і самостійно працювати.
Міжпредметні зв’язки: проекційна
геометрія, архітектура.
Тип уроку: урок засвоєння
нових знань.
Навчально-методичне забезпечення: презентація, ПК, ілюстративний матеріал,
підручник.
Метод навчання:
пояснювально-ілюстративний.
Форма навчання:
Розповідь-пояснення, бесіда.
Хід уроку:
І. Організаційний
момент:
Вчитель
заходить у клас. Взаємне вітання викладача з учнями. Перевірка присутніх та
готовності дошки і робочого місця до заняття. Налаштування ПК для перегляду
презентації.
ІІ. Мотивація навчальної діяльності:
Курс
«Креслення і перспектива» передбачає вивчення загальних понять про проекції,
побудову аксонометричних проекцій, перспективи тощо. Сьогодні тема уроку є
вступною до вивчення всього розділу про проекції. Знання даного матеріалу
допоможуть вам легко впоратись з вивченням подальшого матеріалу.
ІІІ. Повідомлення
теми, мети і завдань уроку:
На
попередніх уроках ви вже вивчали типи шрифтів, будували геометричні лінії та
фігури, циркульні та лекальні криві лінії. Сьогодні ми починаємо вивчати нову
тему: Проекційне креслення: способи
зображення предметів. Прямокутні проекції, їх назви, площини проекцій і
утворення. (Учитель оголошує і записує тему
на дошці).
IV. Актуалізація
опорних знань: (Фронтальне
опитування)
–
Що собою являє синосоїда? Зобразити графічно на дошці синусоїду. (Синусоїда - плоска крива, що задається в
прямокутних координатах певним рівнянням).
– Що таке циклоїда? Зобразити графічно на дошці циклоїду. (Циклоїда – плоска
трансцендентна крива. Вона визначається кінематично як траєкторія фіксованої
точки кола радіуса, що котиться без ковзання по прямій).
– Розкажіть про спіраль Архімеда. Зобразити графічно на дошці спіраль. (Спіраль Архімеда — крива, яку описує точка
M під час її рівномірного руху зі швидкістю v уздовж прямої, що рівномірно
обертається в площині навколо однієї зі своїх точок О із кутовою швидкістю ω.
Спіраль названо ім'ям Архімеда, який вивчив її властивості).
V.
Вивчення нового матеріалу:
Зображення
на фронтальній площині проекцій приймається як головне. Допускається застосовувати
додаткові площини проекцій. При цьому побудови виконують способом заміни площин
проекцій, викладеним у нарисній геометрії.
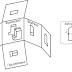
Рис.
10.1 – Розгортка граней куба, які є площинами проекцій
Рис.
10.2 – Основні види, їх назва та розташування на кресленні
Оформлення
ортогонального креслення виконується за стандартом, який позначається як ГОСТ
2.305–2008, і називається: “ЕСКД. Изображения – виды, разрезы, сечения”.
Відповідно до цього стандарту зображення на ортогональному кресленні залежно
від змісту поділяють на види, розрізи, перерізи.
Види
Вид – зображення зверненої до
спостерігача видимої частини поверхні предмета. Невидимі частини предмета не
показують на виді, тобто в загальному випадку на виді відсутні штрихові лінії.
Для зменшення кількості зображень допускається показувати на видах необхідні
невидимі частини предмета за допомогою штрихових ліній.
Основними називають види,
утворені на основних площинах проекцій: фронтальних, горизонтальних і
профільних. Основні види розташовують на кресленні так, як показано на рис.
10.2, при цьому між основними видами встановлюється точний проекційний зв'язок.
Точка А, зображена на рис.10.2, лежить на поверхні деталі. Розташування її
проекцій ілюструє основні правила проекційного зв'язку. Якщо частину предмета
неможливо показати на основних видах без спотворення форми і розмірів, то
застосовують додаткові види, що одержуються на площинах, не паралельних
основним площинам проекцій.
Додатковий вид
позначається як правило написом типу “Б”, а біля зв'язаного з ним зображення предмета
ставиться стрілка, що вказує потрібний напрямок зору. Біля початку стрілки
пишеться та ж сама літера.
Прямокутні
проекції називають також ортогональними. Слово ортогональний походить від
грецьких слів orthos – прямий і gonia – кут. Прямокутні проекції є основними
при складанні технічних креслень. Сутність цих проекцій полягає в тому, що проектований
предмет припускають розташованим між площиною проекцій і спостерігачем. При
цьому промені, що йдуть від спостерігача до площини проекцій, складають з нею
прямі кути.
Площини проекцій
По зображенню
предмета на одній площині проекцій у багатьох випадках не можна судити про його
форму і розмірах. Предмети, показані на рис. 4.3, - прямокутна пластинка,
трикутна призма, прямокутний паралелепіпед і паралелепіпед з частиною циліндра,
- дають у цьому випадку однакові проекції у вигляді прямокутника.
За однією проекції можна судити лише про двох вимірах предмета.
Але й дві проекції предмета часто недостатньо повно відображають його
форму. Так, наприклад, дві проекції прямокутного паралелепіпеда (рис.
4.3, а, б) неоднозначно відображають його форму. Такі дві
проекції можуть мати і трикутна призма (рис. 4.3, в), і призма
з заокругленням (рис. 4.3, г), і т.д.
Рис. 4.3. Проекції
різних за формою предметів на одну площину
Щоб отримати повне уявлення про форму та розміри предмета, його потрібно
спроектувати на дві, три або більше площин. Для простоти проектування ці
площини розташовують взаємно перпендикулярно. Таким чином, три площини
утворюють прямий тригранний кут (рис. 4.4, а). Кожній площині дано назва та
позначення (рис. 4.4б а, б).
 На рис. 4.4, а зображений тригранний кут. Його грані
взаємно перпендикулярні і не лежать в одній площині. Однак креслення виконується
на площині. Для того щоб зображення, отримані на сторонах тригранного кута,
опинилися в одній площині, дві грані цього кута розгортають до суміщення з
третьої гранню, тобто до такого стану, коли всі три площини тригранного кута
опиняться в одній площині. Для цього горизонтальну площину повертають навколо
осі х вниз на 90 °, профільну площину - навколо осі z на
90 ° вправо, як показано стрілками. Тоді обидві ці площини поєднуються з
нерухомою фронтальний. При цьому горизонтальна площина розташовується під
фронтальної, а профільна - праворуч від неї (рис. 4.4, б). Вісь у ніби розпадається на дві: у і у 1. Лінії, що обмежують площини проекцій квадратами, взяті умовно і значення не
мають, тому їх зазвичай не проводять. Тоді площини проекцій зображатимуть, як
показано на рис. 4.4, в.
На рис. 4.4, а зображений тригранний кут. Його грані
взаємно перпендикулярні і не лежать в одній площині. Однак креслення виконується
на площині. Для того щоб зображення, отримані на сторонах тригранного кута,
опинилися в одній площині, дві грані цього кута розгортають до суміщення з
третьої гранню, тобто до такого стану, коли всі три площини тригранного кута
опиняться в одній площині. Для цього горизонтальну площину повертають навколо
осі х вниз на 90 °, профільну площину - навколо осі z на
90 ° вправо, як показано стрілками. Тоді обидві ці площини поєднуються з
нерухомою фронтальний. При цьому горизонтальна площина розташовується під
фронтальної, а профільна - праворуч від неї (рис. 4.4, б). Вісь у ніби розпадається на дві: у і у 1. Лінії, що обмежують площини проекцій квадратами, взяті умовно і значення не
мають, тому їх зазвичай не проводять. Тоді площини проекцій зображатимуть, як
показано на рис. 4.4, в.
VI. Закріплення набутих знань: (Фронтальне опитування)
– Скільки існує площин для побудови прямокутної проекції?
Назвіть їх.
– Які вигляди проекціюють ці площини?
– Яку іншу назву має кожна із проекцій?
VIІ. Підведення підсумків уроку (рефлексія),
оцінювання учнів.
VIІІ. Повідомлення домашнього завдання: вивчити тему за
конспектом.





У Вашому уроці зібрана вся важлива інформація з теми. Дякую за доречні завдання, що підібрані до інформації.
ВідповістиВидалити